The Target Model class is the gateway into the target program for the host application to interface with. Once the host application’s target controller has either started a local target or connected to a remote target, the framework manages the Target Model to keep it in sync with the target. One way that the host application interacts with the target application is through so-called variable binding, where any statically linked (non-stack/non-allocated) variable in the target is synchronized with a corresponding variable in the C# target model class at runtime. Once the target application is compiled and built, the Virtuoso framework uses the target-specific plugin to analyze the target build and extract all information about it, including functions and statically linked variables. The user then uses Virtuoso to configure the Target Model with application-specific variable bindings based on the user’s needs. After every time the target is built, the Virtuoso framework analyzes and extracts information about the target in the background, including all functions and statically linked variables. The user can then use the “Target Model Builder” built into Virtuoso to configure the runtime model for the target.

In the above case, there could be hundreds or thousands of variables in the application, but let’s say we are only interested in interacting with MyInt and MyFloat. We would then specify the MyInt and MyFloat variables as variables that we want to expose to our Target Model (a C# class in this case), and the Target Model Builder tool then “renders” TargetModel.cs, meaning that the Target Model Builder creates or updates the TargetModel.cs source file based on the target hosting settings. Thus, Virtuoso is completely responsible for managing all contents of the TargetModel.cs file. When the host runs, it then launches the target(s) being hosted and creates a Target Model class instance that is available to the host application (again, in this case a C#/.NET WPF desktop application), with properties which stay in sync with their corresponding target variables at runtime. If one of the variables is updated in the target application, the corresponding property on the Target Model gets updated automatically. Conversely, if the host application writes a new value to one of the Target Model properties in C#, the corresponding variable gets updated in the target, at runtime, instantaneously and automatically. Keep in mind that the target application doesn’t need to have any kind of special structure for the binding to work. As far as the target application knows, it’s simply working with a normal variable or buffer in memory.

Virtuoso comes with standard type binding, meaning that an “int” in the target C application can be exposed as an “int” in the C# Target Model as well. However any user-defined data type or structure can be used and exposed as a byte array on the C# Target Model, and then the host application can retype the binding in any way needed.

“Begin by creating a new host application to host the target. Run Virtuoso by clicking the Virtuoso symbol on the desktop, and you will see the Virtuoso Project Browser. Select the New Project tab, select the Visual Studio version you prefer, then specify the folder and host name. We will create a “Hello World” host project on the desktop. Click “Create Project” and your Virtuoso host, with corresponding C# application, will be created.”

After your host is created, you will see your empty host schematic for the HelloWorld host as shown below.

Click on the “Open In IDE” button to open the host in Visual Studio. You will see your C# “HelloWorld” project, a completely normal C# MVVM desktop application.

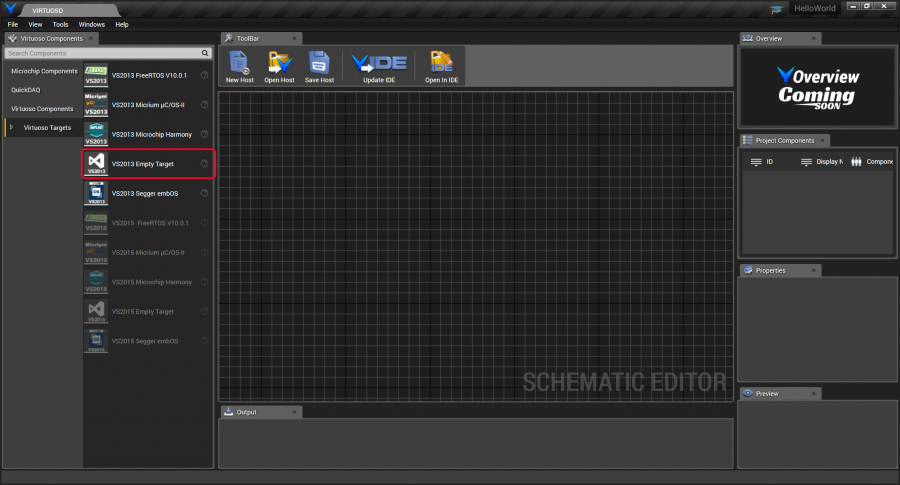
With Visual Studio still open, go back to the schematic editor. Select the Virtuoso Targets component group and you will see your available target templates. These options might look different for you depending on which target template Montage packages you have installed in your vault. Add an empty target by dragging and dropping the VS2013 Empty Target onto the schematic as shown below.

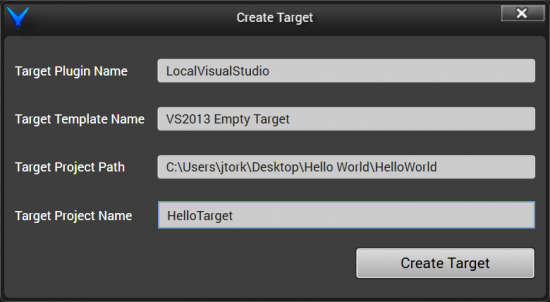
After dragging and dropping, you will be prompted to specify the name of the target. Give it the name “HelloTarget” as shown below and click “Create Target”.

The target will be represented on the schematic as a component as shown below, initially with only the default power ports.

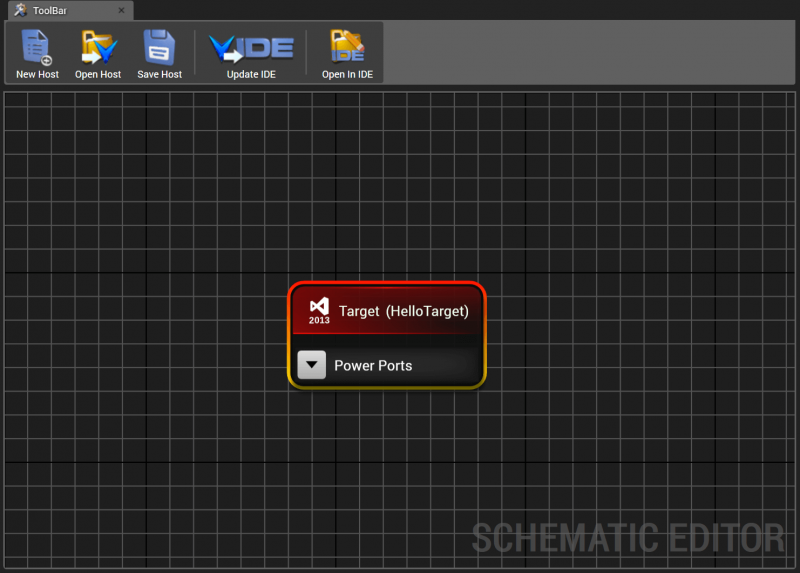
Click the “Open In IDE” button again to pull up the Visual Studio Solution. In the solution explorer window, you will see a “HelloWorld” C# project (green) and a “HelloTarget” C++ project (purple), as shown below. Click Build->Build Solution to verify that both projects in the solution build successfully.

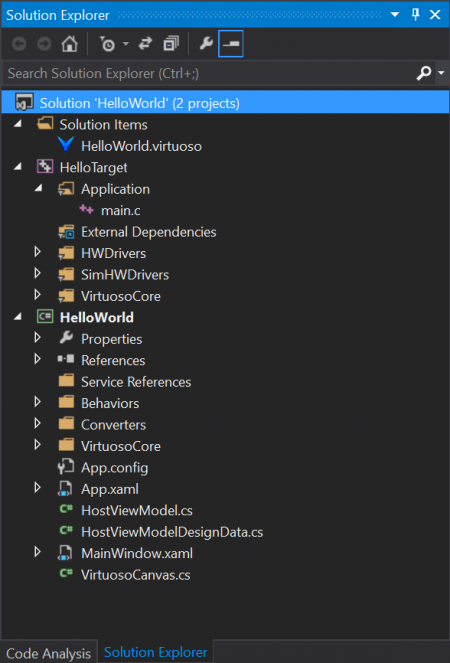
In the C# project, expand the “VirtuosoCore” folder and note the “HelloTargetModel.cs” file. This is the runtime model class for the target, and was generated along with the C++ “Target” project when you created the target. If you had named the target “MyCoolApp”, then you would instead see “MyCoolAppModel.cs” and a C++ project named “MyCoolApp”.

Open the HelloTargetModel.cs file and notice that it has constructors, a few fields, and a bool property named “PowerInput”.

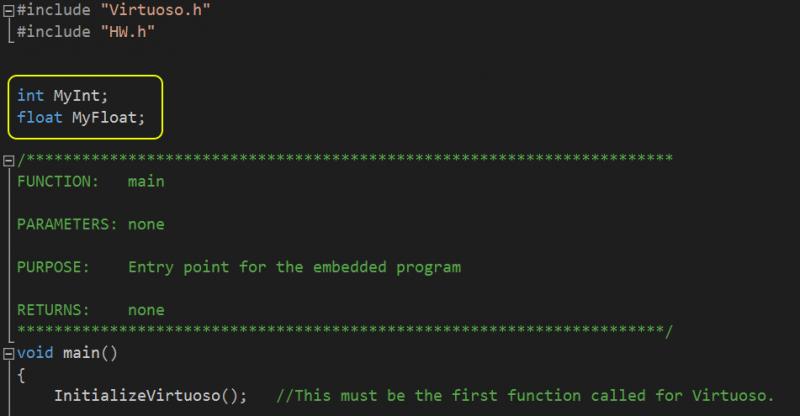
With this file still open, now expand the “Application” folder in the Target project, and open main.c. Above the main function, declare the statically linked MyInt and MyFloat variables as an ‘int’ and a ‘float’, respectively, as shown below.

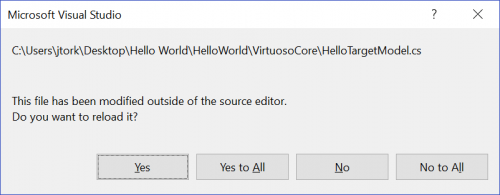
Now select Build->Build Solution from the menu or press F6 to build the solution. In the Output window you will see that one project built successfully (the C# project didn’t need to be rebuilt because it didn’t change), and you may get a message notification as shown below informing you that the file inside this editor was changed externally. This is because you have the HelloTargetModel.cs file open, and when you rebuilt the Target project, Virtuoso rewrote this HelloTargetModel.cs file. Thus, any changes made to HelloTargetModel.cs will be overwritten by Virtuoso, and you shouldn’t make any changes to this file. Click Yes or Yes to All to continue.

Select the TargetModel.cs file in the window tab, and you will note that while the TargetModel.cs file was re-rendered, it is the same as it was before. This is because we haven’t selected any C variables to be exposed on the target model. We will do so now. In the “Solution Items” folder in the Solution Explorer window, double-click on the target file, “Target.virtuosotarget”. This will open up the Target Model Builder for this target, as shown below.

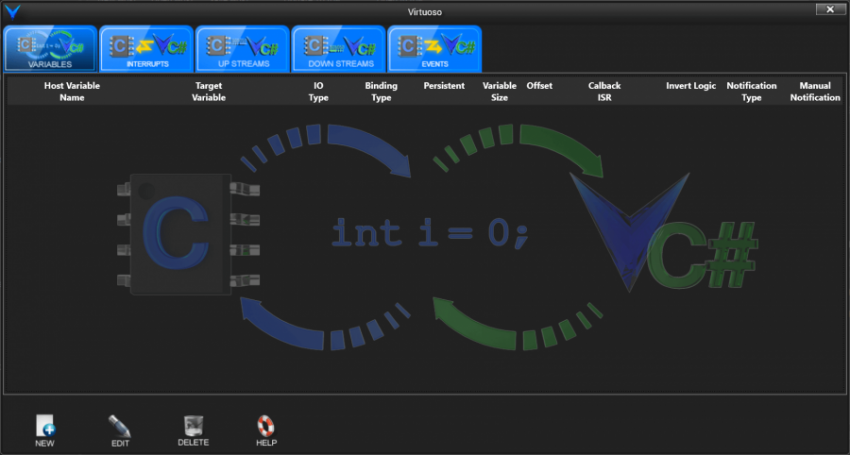
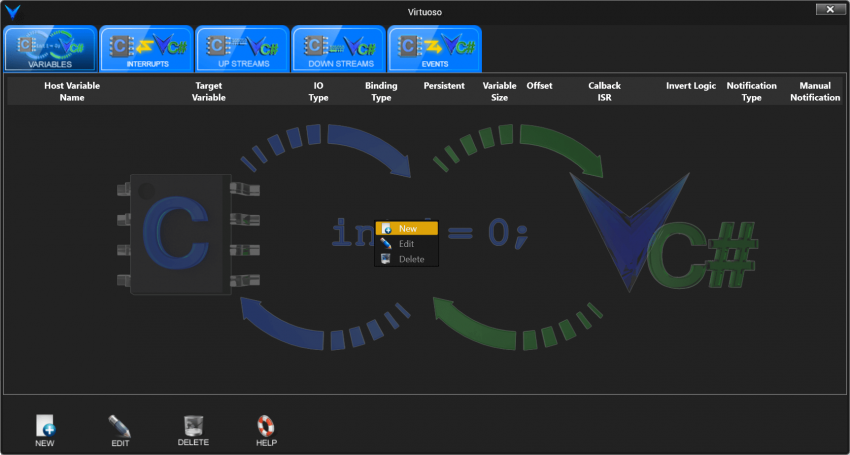
The tab that is selected by default is the “Variables” tab, and this is the one we’re interested in. Click the “New” icon in the lower left corner of the Target Model Builder window, or right click in the table area and click “New” in the context menu, as shown below.

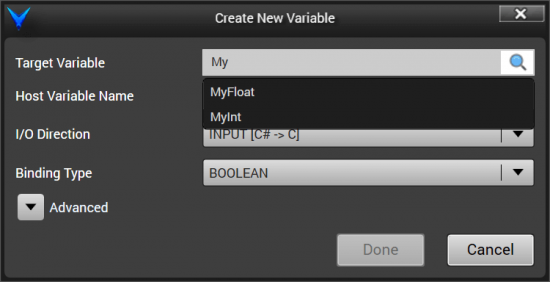
This opens up the “Create New Variable” window, where we can create a new variable binding between the host and the target. In the “Target Variable” textbox, start typing “My” and you will see the two statically linked variables we declared, MyInt and MyFloat, as filtered options.

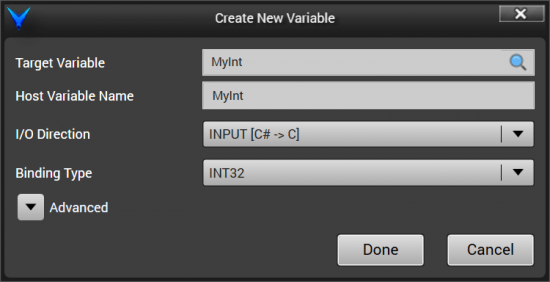
Select MyInt. The “Host Variable Name” field will be filled in with “MyInt” by default, and generally you will want to use the same name. This is the name of the variable that will be rendered on the Target Model C# class to represent this variable in C#. The I/O Type specifies whether we want this variable binding to be an INPUT (the C# property will be written to, and the value will be updated in the C target), an OUTPUT (any time the variable is written to in C, the C# property will be automatically updated), or BIDIRECTIONAL (the variable can be written to from either C or C#, and the change will be reflected in the other). Leave this variable as an INPUT. The Binding Type indicates what variable type the C target variable will be presented as in the C# Target Model. Change this to INT32 and click “Done”.

You will now see this variable binding in the Variables binding list, as shown below.

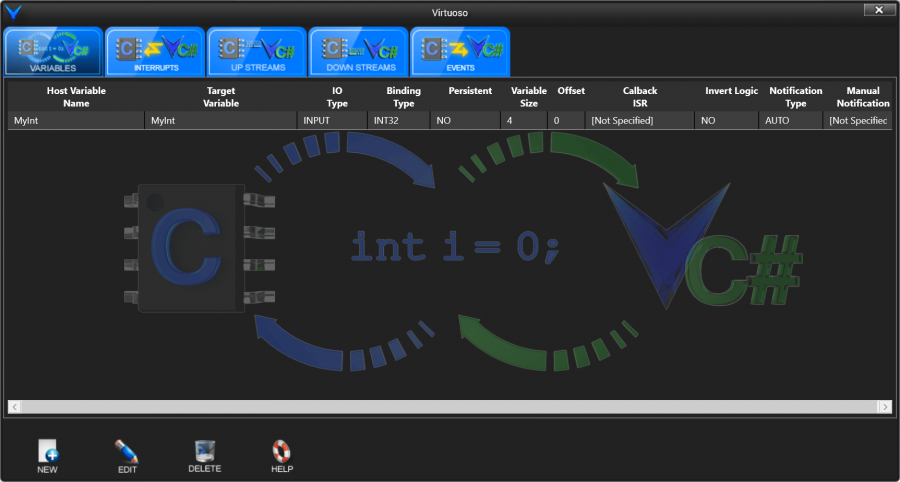
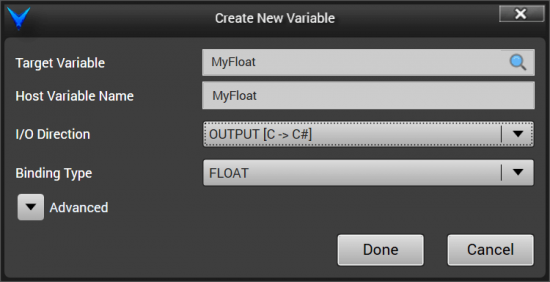
Click “New” again to create another new variable binding and select MyFloat as an OUTPUT with a FLOAT binding type, as shown below, and click “Done”.

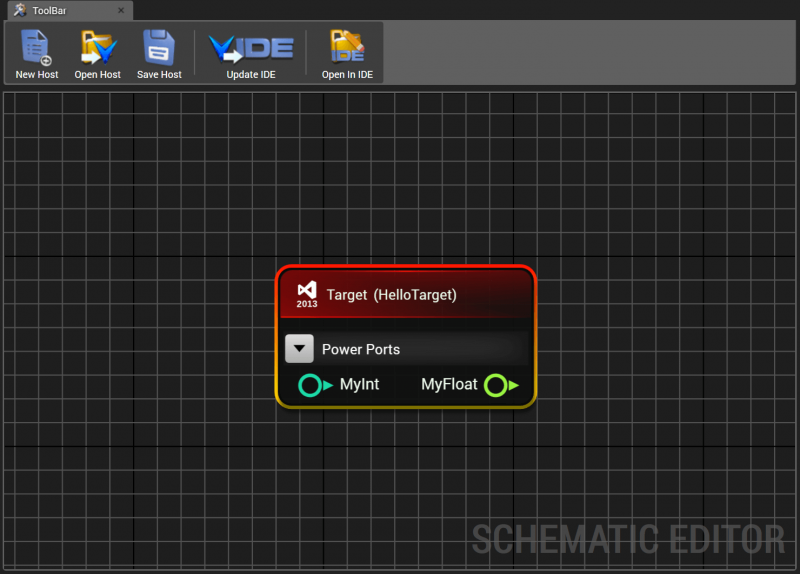
You will now see both variables listed in the Target Model Builder Variables table. Click the close button in the top right corner of the Target Model Builder window to close the Target Model Builder. The Target schematic component will now be updated to have a MyInt input port and a MyFloat output port as shown below.

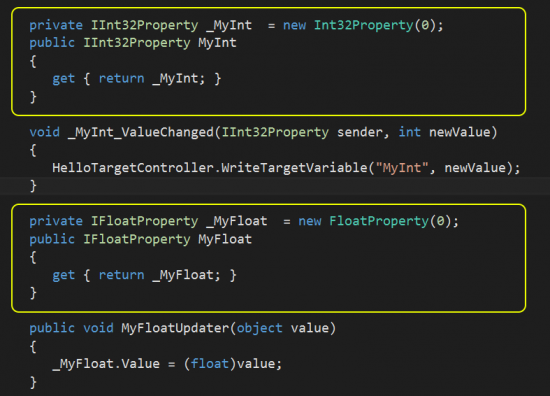
Click the “Update To IDE” button. If the HelloTargetModel.cs file is still open, you will notice that the message is displayed again indicating that the HelloTargetModel.cs file was changed externally. Click “Yes” and look at the contents of HelloTargetModel.cs. You will see that there are now two properties added to the HelloTargetModel.cs class: a MyInt property and a MyFloat property, of type IInt32Property and IFloatProperty, respectively. Each of these property interfaces have a Value getter and setter which provide access to the underlying Int32 and float values. Exposing the variables using property interfaces instead of direct properties is for performance reasons. They could be exposed directly as Int32 and float properties. These C variables can now be accessed directly on the C# target model by any C# code in the host.

We have now successfully created a C# host project and a hosted C/C++ target project and configured variable bindings for statically linked properties. The project can be built and run, although it doesn’t do anything exciting quite yet. But as we will see, this will be one of the foundational functionalities that make the composition of virtual devices very easy.